Leonard Susskind, Stanfordova univerzita. Foto: Luboš Motl, http://motls.blogspot.com

Co se stane, když hodíte slona do černé díry? Zní to jako špatný vtip, ale je to otázka, nad kterou si láme hlavu Leonard Susskind, strunový teoretik ze Stanfordovy univerzity v Kalifornii. Lenny se snaží slona zachránit několik desítek let. Konečně, jak tvrdí, našel způsob, jak toho docílit. Ovšem důsledky jeho objevu otřásají našimi představami o prostoru a času. Jsou-li jeho výpočty správné, slon musí být na více místech najedou.

V každodenním životě je lokálnost samo sebou dána. Jste tam, já jsem zde; nikdo z nás není zároveň na více místech. I v Einsteinově teorii relativity, kde se vzdálenosti a časové intervaly mění v závislosti na vztažné soustavě pozorovatele, je poloha objektů přesně definovaná. Susskind však tvrdí, že lokálnost v klasickém smyslu je jen mýtem. Nic není takové, jak se zdá. Či spíše nic není tam, jak to vypadá.

Otázka, jíž Susskind řešil, není jen „zábavným“ hlavolamem. Říká nám něco o samotném chování vesmíru. Ač to může znít podivně, osud slona v černé díře má hluboké důsledky pro kvantovou gravitaci, teorii, v níž se fyzici snaží spojit teorii popisující svět elementárních částic — kvantovou mechaniku — a teorií popisující vesmír na největších měřítkách —obecnou teorii relativity, dva základní pilíře moderní fyziky. Černé díry díky své ohromné gravitaci a jiným vlastnostem jsou už dlouhou dobu živnou půdou pro teoretizování o těchto problémech.

Informační paradox černých děr

Vše začalo v polovině 70. let, kdy známý teoretický fyzik Stephen Hawking z Cambridžské univerzity ve svých výpočtech ukázal, že černé díry nejsou tak úplně černé. Zjistil, že vysílají záření. Ve skutečnosti se pozvolna vypařují, po miliardy let pomalinku mizí. Toto Hawkingovo záření má svůj původ v kvantových jevech (v tzv. Heisenbergově principu neurčitosti). Vychází z horizontu událostí, oblasti, ze které není úniku. Hawking položil otázku: jestliže se nakonec černá díra zcela vypaří, co se stane s hmotou (hlavně informacemi o ní), kterou během své existence pohltila? Buďto může opět uniknout do vesmíru se zářením, nebo může dočista zmizet.

Problém je v tom, že zákony fyziky ani jednu možnost nepovolují. „Čelíme složitému paradoxu, který se odvíjí od skutečnosti, že každý možný výsledek týkající se vypařování černých děr je v rozporu s určitými důležitými aspekty fyziky,“ řekl pro časopis New Sicentist Stever Gidding, teoretik z Kalifornské univerzity v Santa Barbaře.

Mezi fyziky se tomuto problému říká informační paradox černých děr. Paradox je to proto, protože kvantová fyzika zakazuje, aby se informace ztrácely, přesto však i scénáře úniku informací z černých děr vypadají rozporuplně. Fyzici často hovoří raději o informacích než samotné hmotě, protože informace je považována za fundamentálnější pojem.

V kvantové mechanice informace, která popisuje stav částice, nemůže dírami rovnic jakkoliv proklouznout. Pokud by to bylo možné, šlo by o matematickou noční můru. Schrödingerova rovnice popisující vývoj kvantového systému v čase by ztratila na významu, protože by byla narušena kauzalita (pojmy „před“ a „po“ by ztratily na významu, smíchal by se „následek“ s „příčinou“) a jakékoliv předpovědi plynoucí z rovnice by byly absurdní. „Fyzika jako taková stojí na skutečnosti, že informace se zachovává, ať už v jakkoliv skryté formě,“ říká Susskind.

Po desetiletí byl ale Stephen Hawking přesvědčený, že informace se v černé díře ztrácí, protože — jak upozorňoval — uvolněné záření mělo náhodný charakter a nemohlo obsahovat žádné informace o hmotě, která do černé díry spadla. V roce 1997 společně s Kipem Thornem z Kalifornského technického institutu (Caltech) ohledně této otázky uzavřeli sázku s Johnem Preskillem, také z Caltechu. Vsadili se o encyklopedii baseballu. Ticho po pěšině bylo až do června 2004, když na konferenci v Dublinu Hawking překvapivě přiznal, že se mýlil a že informace se nakonec uchovat může. Preskill tak sázku vyhrál.

Vesmír coby iluze

Co stálo za tím, že Hawking změnil názor? Byla to práce mladého teoretika Juana Maldaceny z Institutu pokročilých studií v Princetonu, New Jersey, USA. Jeho jméno sice není mezi širší veřejností příliš známé, ale tento mladý fyzik je autor jedné průkopnické práce na poli teorie superstrun, teorie, která je dnes hlavním kandidátem na takzvanou teorii všeho.

V roce 1997 Maldacena vyvinul typ superstrunové teorie existující ve světě s pěti velkými dimenzemi (náš svět má velké rozměry tři) a s typicky zakřiveným prostoročasem. Ukázal, že jeho teorie — která zahrnovala i gravitaci — je ekvivalentní s obyčejnou kvantovou teorií pole, bez gravitace, žijící na čtyřrozměrné hranici onoho pětirozměrného světa. Interakce částic na čtyřrozměrné hranici přesně odpovídají interakcím strun uvnitř pětirozměrného světa. Ač předchozí věty mohou znít složitě, zjednodušeně lze říct, že děje odehrávající se „uvnitř“ pětirozměrného vesmíru (s gravitací) jsou nerozlišitelné od dějů na méněrozměrné hranici (bez gravitace).

Jde o vskutku zarážející závěr. Oba světy (čytřrozměrná hranice a pětirozměrný svět) přece vypadají velmi odlišně. Přesto jejich informační obsah je identický. Pro lepší představu si můžeme představit třeba obyčejný nafukovací balonek. Vše, co se odehrává ve třech rozměrech vzduchu uvnitř balonku je nerozeznatelné od dějů na dvojrozměrném povrchu balonku.

Hmota uvnitř pětirozměrného světa, tvořená vícerozměrnými strunami, pak může být prezentována jako holografická projekce kvantových částic na čtyřrozměrné hranici. Jde o něco podobného jako v případě obyčejného hologramu, kdy laser při ozáření dvojrozměrné destičky vytvoří trojrozměrný obraz. Laser tak z informací ukrytých ve dvou rozměrech poskládá vícerozměrný (trojrozměrný) obraz. Ačkoliv Maldacenův vesmír se od našeho velmi liší, přece jen elegance teorie napovídá, že i náš kosmos by mohl být jen iluzí — mohl by také být obřím hologramem.

S myšlenkou, že vesmír je hologramem, přišli nejprve právě Lenny Susskind, zakladatel strunové teorie, a nositel Nobelovy ceny Gerard ‚t Hooft. Oba použili poznatku, že entropie (míra neuspořádanosti systému, tedy i míra informačního obsahu) černé díry je přímo úměrná povrchu černé díry a ne jejímu objemu. Ovšem Maldacena explicitně ukázal, jak by holografický vesmír mohl fungovat a — což je rozhodující — proč informace se v černé díře nemůže ztrácet.

Podle jeho teorie má černá díra, ostatně jako cokoliv jiného, své „druhé já“ žijící na okraji vesmíru. Ukazuje se, že vypařování černé díry odpovídá kvantovým částicím interagujícím na této hranici (vzpomeňte si na nafukovací balonek). Jelikož se žádná informace nemůže v reji obyčejných kvantových částic ztratit, nemůže docházet ani k žádnému záhadnému zničení informací v černých dírách. „Hraniční teorie respektuje zákony kvantové mechaniky,“ říká Maldacena. „V merku má všechny informace.“

Jistěže náš vesmír má do vesmíru, s nímž pracoval Maldacena, velmi daleko. Ale ty výsledky, které Maldacena získal, jsou natolik pozoruhodné, že někteří fyzici „holografický princip“ a jeho výsledky plně přijímají. „Opozice, včetně Hawkinga, musela ustoupit,“ říká Susskind. „Holografický princip je natolik matematicky přesný, že z praktických důvodů skoro všichni teoretičtí fyzici došli k závěru, že může být pravdivý stejně jako zachování informací, které z něj plyne.“

Kam se informace schovaly?

Dobrá, zůstává však jeden závažný problém: pokud se informace v černé díře neztrácí, kde je? Vědci spekulují o tom, že je zakódovaná do záření vycházející z černých děr. „Myšlenka je ta, že Hawkingovo záření nemá nahodilou povahu, ale obsahuje informace o hmotě, která do díry spadla,“ říká Maldacena.

Susskind jde ještě o kousek dál. Jelikož holografický princip nedává prostor k tomu, aby se informace ztrácela, tvrdí, že ani žádný pozorovatel by neměl vidět informace se ztrácet. Zde je jeho myšlenkový experiment (ve kterých si velmi liboval například i sám Einstein).

A tak se dostáváme zpět ke slonovi. Představme si dva pozorovatele, jednoho, který sleduje černou díru z bezpečné vzdálenosti a druhého, který sedí na zádech slona padajícího do černé díry. První pozorovatel vidí, jak se slon rychle blíží do gravitační pasti. Zpočátku se slon bude z hlediska tohoto pozorovatele blížit k černé díře velmi rychle, ale jeho pohyb se bude zpomalovat, a to díky zpomalování času, které je způsobeno silným gravitačním polem černé díry. První pozorovatel díky tomuto efektu nikdy nespatří slona překročit horizont událostí černé díry, oblast, ze které už není návratu (ani světlo z pod horizontu událostí nemůže uniknout). Namísto toho tento pozorovatel bude tvrdit, že chudáka slona na popel spálilo Hawkingovo záření. A podle něj taky „popel“ obsahuje informace o slonovi.

Na dvou místech naráz

Tu však do našeho příběhu přichází zvrat. Druhý pozorovatel sedící na slonovi totiž se slonem horizont událostí černé díry projde. Horizont událostí není žádnou stěnou v prostoru. Jde prostě jen o oblast v prostoru, z pod které není schopno nic uniknout. Z pod něj žádný vzdálený pozorovatel neuvidí unikat ani světlo (proto jsou černé díry „černé“). Pro padajícího pozorovatele však není ničím výjimečným. Pohroma pro něj přijde, až se přiblíží k singularitě, „středu“ černé díry. Kolem singularity je gravitace natolik silná, že slona i pozorovatele roztrhá na kousíčky. Ovšem ani tento pozorovatel po dobu svého pádu nepozoroval žádnou ztrátu informací. Dle něj se zachovává.

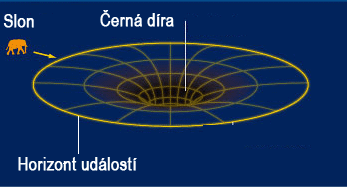
Slon se blíží k černé díře…

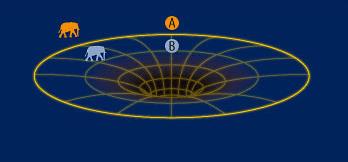
První pozorovatel (A) nacházející se v bezpečné vzdálenosti od černé díry vidí slona se čím dál víc blížit horizontu událostí. Podle něj nikdy tuto hranici nepřekročí. Druhý pozorovatel (B) padající se slonem však pozoruje, že slon se přes horizont událostí dostane bez problémů.

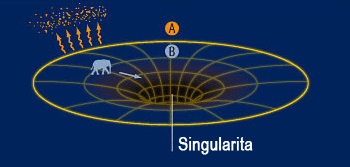
Pozorovatel (A) během dlouhé doby pozoruje, že slona na popel spálí Hawkingovo záření, kdežto pozorovatel (B) je se slonem v černé díře a dále padá.

Žádný z příběhu sice nekončí zrovna šťastně, ale i přesto se musíme ptát: který je správný? Který popisuje to, k čemu skutečně dochází? Přece podle prvního pozorovatele slon nikdy nepřekročí práh horizontu událostí, podle druhého pozorovatele v tom není problém. Odpověď vás možná překvapí, ale zákony fyziky mluví jasně: oba příběhy jsou správné. Dozajista vás to zarazí, vždyť jeden příběh vylučuje scénář druhého. Je slon uvnitř, nebo venku?

Susskind odpovídá jasně. Slon je na obou místech. Záleží jen na tom, koho se zeptáte. „Došli jsme k tomu, že nemůžete hovořit o tom, co je za horizontem událostí a co je před ním,“ říká. „V kvantové mechanice je normální, že spojku „a“ nahradíte za „nebo“. Třeba takové světlo je vlněním nebo proudem částic. Záleží jen na tom, jaký experiment zrovna provádíte. Elektron má určitou pozici nebo má hybnost (součin rychlosti a hmotnosti) v závislosti na tom, co měříte. Totéž se děje s černými děrami. Buďto popisujeme to, co spadlo za horizont v jazyce toho, co za horizontem je, nebo to popisujeme v jazyce Hawkingova záření, které z černé díry vychází.“

Kvantová kopírka neexistuje

Možná vás ale také napadne následující. Třeba existují dvě kopie informace. Možná když se slon přiblíží k horizontu událostí, vznikne jedna jeho kopie. Pak „originál“ zůstane stát kousíček před horizontem a „kopie“ spadne do černé díry. Ač tato úvaha může pro někoho znít zajímavě, tak vězte, že není správná. Z kvantové mechaniky víme, že k tomu dojít nemůže. Existuje jakási věta o „neexistenci klonování“ (myšleno v kvantovém smyslu). Není těžké ukázat, že skutečně neexistuje možnost, jak „zkopírování“ docílit. To také Leonard Susskind potvrzuje: „Neexistuje žádná kvantová kopírka.“ Takže tentýž slon se musí nacházet na dvou místech najednou: živý za horizontem a mrtvý v hromadě žhnoucího popela těsně před horizontem.

Jde o skutečně překvapivý závěr. Ovšemže na poli kvantové mechaniky platí něco podobného. Polohy a rychlosti částic nejsou pevně dány — vše, co fyzici pracující s kvantovou mechanikou mohou dělat, je určovat pravděpodobnosti výskytu částic —, ale je potřeba si uvědomit, že kvantová mechanika takto pevně vládne na malinkých vzdálenostech, ve světě elementárních částic. Teď hovoříme o něčem mnohem větším, o něčem z makrosvěta. Kdyby taková černá díra byla obrovská, „dvě verze slona“ by od sebe mohly být vzdáleny na miliardy světelných let. „Lidé si často myslí, že kvantová neurčitost je jevem malých vzdáleností,“ říká Susskind. „My ale zjišťujeme, že v místech, kde je role kvantové gravitace stále důležitější, kvantová neurčitost se dostává do větších měřítek.“

Nová forma relativity

To vše odpovídá skutečnosti, že poloha objektu v prostoru není jednoznačná. Susskind to nazývá „novou formou relativity“. Einstein vzal věci, o kterých si lidé mysleli, že jsou neměnné — délka předmětu, plynutí času… — a ukázal, že jsou relativní. Poloha objektu v prostoru nebo času může být definována pouze vzhledem k pozorovateli, jeho poloha v časoprostoru byla ale jednoznačná. Nyní se však podle Susskinda i tento pojem otřásá v základech — poloha objektu v časoprostoru závisí na pohybovém stavu pozorovatele vzhledem k horizontu událostí.

A co víc, tento nový typ nelokálnosti neplatí jen pro černé díry. Nelokálnost se vyskytuje všude tam, kde hranice odděluje dvě oblasti prostoru, které spolu nemohou komunikovat. A tyto hranice jsou běžnější, než si možná myslíte. Cokoliv, co se pohybuje zrychleně, ať už Země, sluneční soustava nebo třeba Mléčná dráha, vytváří podobné horizonty také. I když si jdete zaběhat, existují kolem vás oblasti prostoru, ze kterých by se k vám nikdy nedostalo světlo (onen nejrychlejší poslíček informací), pokud byste pořád zrychlovali. Tyto nedosažitelné oblasti leží za vaším horizontem.

Je možné, jak si Susskind přeje, že nový typ nelokálnosti pomůže fyzikům s vývojem kvantové teorie gravitace, teorie spojující zákony malého (kvantové mechaniky) a teorie velkého (Einsteinovy obecné teorie relativity). Kupříkladu kvantová gravitace by se mohla řídit holografickým principem. „Musí to být součást chápání kvantové gravitace,“ říká Giddings. „Je pravděpodobné, že informační paradox černých děr povede k revoluci přinejmenším takové, jakou bylo zrození kvantové mechaniky.“

To není vše. Skutečnost, že časoprostor samotný zrychluje — čili že se zrychluje rozpínání kosmu — znamená, že i vesmír vytváří horizont. Stejně jako bychom mohli dekódováním Hawkingova záření zjistit, že slon zmizel uvnitř černé díry, možná se můžeme dozvědět, co je za naším kosmickým horizontem dekódováním jeho záření. Jak? Podle Susskinda reliktní záření (mikrovlnné záření, jež je dozvukem velkého třesku), které nás obklopuje, může být mnohem důležitější, než si někteří dokáží připustit. Kosmologové toto záření studují proto, že nám může leccos říct o počátcích času, ovšem Susskind si pohrává s domněnkou, že může jít o druh Hawkingova záření pocházejícího z okraje vesmíru. Jestliže by to byla pravda, může nám povědět něco o slonech z jiných koutů vesmíru.

zdroj: New Scientist