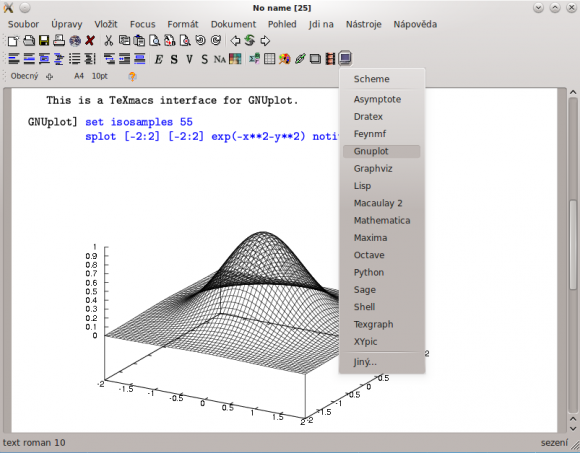
Editor TeXmacs slouží k sazbě dokumentů s matematickými znaky, ale lze v něm provádět i výpočty (voláním matematických systémů a nástrojů nainstalovaných v počítači -- Mathematica, Sage, Gnuplot, Maxima...)

Svět matematických systémů není složen jen z těch zvučných jmen známých komerčních programů, které jsou finančně dost nákladné. Matematici, fyzici a další vědci mají k dispozici řadu výkonného softwaru zcela zdarma. Snad někomu náš malý návod, co „vše“ lze bezplatně využívat na osobním počítači.

Začněme tím jednodušším – v tom smyslu, že takové matematické nástroje se hodí všem uživatelům, kteří tu a tam potřebují něco spočítat, nakreslit grafy apod., aniž by měli sebemenší znalosti skriptování v různých matematických a programovacích jazycích.

Ikonou mezi bezplatnými matematickými nástroji je bezesporu Maxima (s podařeným grafickým rozhraním wxMaxima, jež je součástí instalátoru pro Windows). Uživatelé sice mají možnost vytvářet v rámci Maximy i složitější kusy kódů, ale začátečníkům v prostředí wxMaxima určitě práci ulehčí různá menu a okna, jež potřebné příkazy provedou za ně (například tvorbu grafů).

Nesmíme zapomenout na webovou službu Wolfram|Alpha z dílny Wolfram Research vedeného Stephen Wolframem. Služba pracuje s obrovskými databázemi dat a pro výpočty používá známý matematický software Mathematica.

K provádění výpočtů není nutné znát pravou syntaxi Mathematicy, vstupy lze psát v lidském jazyce. Našinci však budou muset oprášit aspoň minimální znalosti angličtiny. Každopádně zatímco v systému Mathematica byste museli pro výpočet neurčitého integrálu nějaké funkce dodržet syntaxi (dnes už vlastně ne, Mathematica 8.0 je propojena s Wolfram|Alpha) ve tvaru Integrate[f(x),x], v poli Wolfram|Alpha stačí zadat třeba integral f(x) (například zkuste zadat integral sin x nebo také int sin x).

Mocným nástrojem pro tvorbu grafů (2D i 3D) je bezesporu Gnuplot, jehož není mnohým patrně nutné představovat. Nečekejte však žádné „fancy“ grafické rozhraní – pokud Gnuplot nepoužijete v rámci nějakých jiných prostředí či editorů (viz níže), musíte se spolehnout na de facto práci s příkazy (nicméně Gnuplot je využívá i zmíněná Maxima). To sice leckoho může odradit, na druhou stranu práce v příkazovém režimu uživateli otevírá cestu grafy si upravit k dokonalosti podle přání.

Pro numerické výpočty, ve stylu systému Matlab, slouží pokročilé a mocné aplikace GNU/Octave a SciLab, jež jsou využívány i na řadě vědeckých, technických či průmyslových pracovišť (pro milovníky přívětivějších grafických rozhraní: zkuste Octave použít ve slušivém a rozšířeném kabáte napsaném v Qt, tzv. QtOctave – dostupné je i port pro Windows, v linuxových systémech bývá zpravidla v příslušných repozitářích).

Teď jsme se vlastně k tomu složitějšímu, zato bohatšímu. Nejde proto nezmínit programovací jazyk Python a řadu nástrojů, které umožňují provádět spousty náročných matematických aplikací.

SciPy („sájpáj ;-) / Scientific Tools for Python / Vědecké nástroje pro Python), hodně populární vědecký software, který závisí na NumPy, balíku pro numerické výpočty (vše na jednom místě). Milovníci Pythonu pak mají k dispozici také SimPy, další z řad vědeckých balíčků, tentokráte určeného pro simulace. Na webu SimPy se můžeme dočíst, že jde o jeden z nejčistších a nejjednodušších balíčků pro simulace diskrétních událostí. Přesvědčit se o tom vlastně můžete sami.

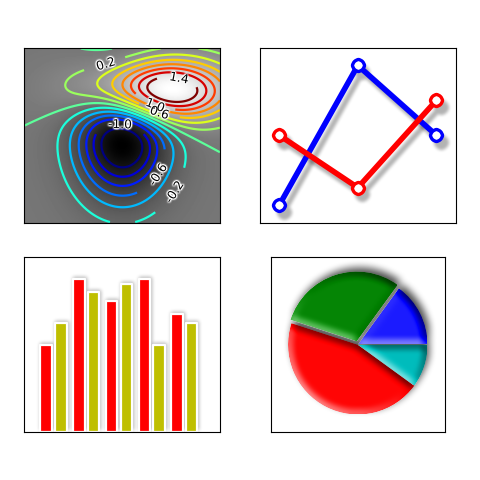
Co se týče grafiky, k úžasným výsledkům vede použití Matplotlib. Je sice primárně určen pro tvorbu dvourozměrných grafů, ale díky nástroji mplot3d v něm lze vykreslovat i 3D-grafiku. Jeho předností je opravdu povedený grafický výstup, který je ozdobou všech publikací. Dalším pythonovským balíčkem je SymPy, který je určen pro symbolické výpočty.

S Pythonem a vědeckými balíčky lze jednak pracovat v rámci konzole (shell iPython), popř. vývojových prostředí, jako je NetBeans a Eclipse (za použití pluginu PyDev) nebo různých editorů.

Ohledně Pythonu a vizualizací bychom zapomenout na další vizualizační software jménem Mayavi (v současnosti Mayavi2), pěkný tutoriál najdete na stránce http://code.enthought.com/projects/mayavi/, Mayavi2 je věnována stránka i na webu SciPy, http://www.scipy.org/Cookbook/MayaVi/RunningMayavi2.

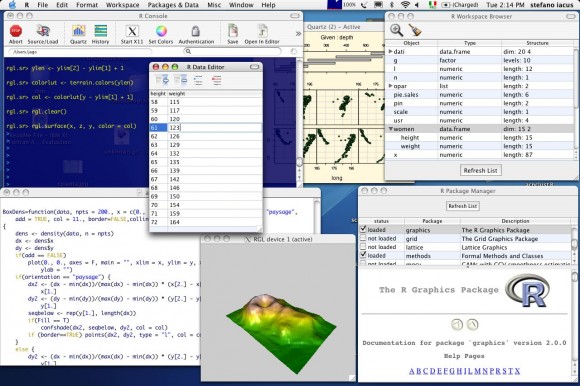
Pro náročnější aplikace a pro zkušenější uživatele je určen další skvělý jazyk s opravdu krátkým názvem: R. Je to dnes vlastně standard mezi statistiky. Najdete jej na stránce http://www.r-project.org. Jeho grafické výstupy rovněž patří mezi to nejlepší, čeho lze na osobních počítačích zdarma dosáhnout.

R v prostředí Mac OS (R-project.org)

To nejlepší jsme si nechali na konec. Uživatelé Windows ale mají docela smůlu, protože třešnička na dortu jménem Sage (SageMath) je dostupná pouze pro operační systémy s jádrem Linuxu a unixový Solaris a Mac OS X. Nicméně na webu SageMath.org je dostupný virtuální obraz pro Vmware a VirtualBox (koneckonců díky obrovským výpočetním silám dnešních osobních počítačů by virtualizace už mohla vcelku zdomácnět).

Sage Math představuje obří systém plný různých matematických balíků a jde v něm dělat prakticky cokoli, co nejen matematik potřebuje. Navíc grafické rozhraní běží v prohlížeči a umožňuje řadu věcí, které obyčejně u podobných systémů dělat ani najde. Jak prostředí vypadá, si můžete prohlédnout na webu http://www.sagenb.org (můžete si vytvořit účet a počítat online, vytvářet projekty, ukládat si je na tamním serveru, sdílet…).

Systém Sage opět využívá Python a jeho syntaxi (je v něm, resp. Cythonu psán). Je složen ze stovky matematických balíků (i mnoha těch, jež jsme zmínili výše). Pythonovské balíky NumPy, SciPy, Sympy, …, Fortran, Maxima, , C++, Matplotlib, Tachyon, jsMath (javascriptová implementace LaTeXu), … Vítejte v Sage Math!

Uživatelům rozšířených operačních systémů, jako je openSUSE nebo Mandriva musíme však říct jedno: smetanu slízlo Ubuntu – nejnovější binárky nejsou pro openSUSE ani Mandrivu dostupné. Pouze pro Ubuntu. Nezbývá vám tak nic jiného než si ze zdrojových kódů Sage zkompilovat sami. Není to nic těžkého (viz soubor readme), horší je to s časem kompilace. Sage Math je opravdu rozsáhlý systém a těch 2,2 GB dá procesorům zabrat. Čas kompilace se samozřejmě odvíjí od vašeho hardwaru (malá motivace: na netbooku s procesorem Intel Atom :) kompilace trvala bezmála 11 hodin.).

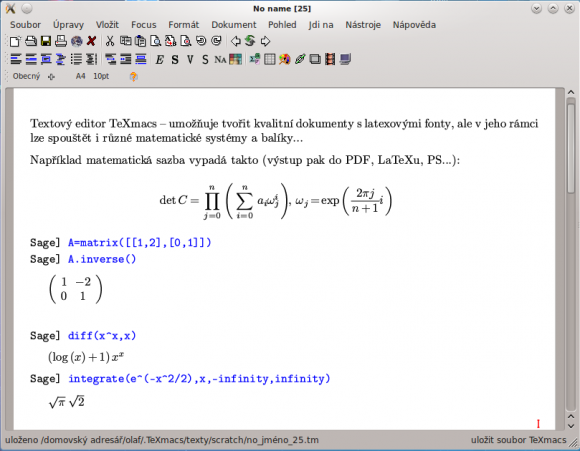
Na úplný závěr ještě dvě třešničky. Spoustu z výše zmíněných (i nezmíněných) matematických systémů a balíčků je možno pohodlně používat v rámci skutečně užitečného textového procesoru TeXmacs. Ten umožňuje vytvářet dokumenty s matematickou sazbou LaTeXovými fonty, ale navíc v těchto dokumentech lze provádět výpočty (přes tzv. sezení, kterými se vyvolají jádra externích matematických systémů). Kromě výše zmíněných nástrojů v něm lze spouštět třeba i Mathematicu, Matlab, ale i třeba i další ještě nezmíněný, zato hodně podařený software Macaulay2, jenž je určen pro algebraickou geometrii a komutativní algebru.

Více podrobněji příště…

Oldřich Klimánek, Scinet.cz pro DSL.cz